El método de nudos

 Buenaas,

Hoy vamos a hablar del método para resolver los esfuerzos en las barras según el método de nudos:

Podéis ver el ejercicio en el siguiente vídeo:

 

A continuación lo resuelvo numéricamente:

Tenemos la siguiente estructura:

Al ser una estructura fija y equilibrada: ∑Fx = 0; ∑Fy = 0 y ∑M = 0

Aunque el apoyo articulado fijo tiene reacciones horizontales, son cero porque no existe ninguna fuerza horizontal u oblicua, solo hay verticales, es decir: ∑Fx = 0 = R1x = R3x = 0

∑Fy = 0 = R1y + R3y -10 kN -10kN = 0

Por simetría se tiene que cumplir que R1y = R3y

Por tanto: R1y + R1y -10 kN -10kN = 0 -> 2R1y  -10 kN -10kN = 0 -> R1y = (20/2)kN = 10kN = R2y

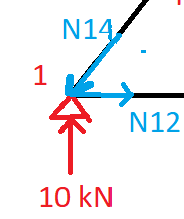
Numeramos los nudos y ponemos las reacciones verticales:

Ahora Calculamos el equilibrio de las fuerzas de las barras en el nudo 1:

∑Fy = 0 = N14*sen60 + 10kN -> N14 =( -10/sen60)kN = -11,54 kN (Mal dibujado, comprime al nudo).

Es decir: 

Ahora calculamos las fuerzas horizontales: ∑Fx = 0 = N12 -N14*cos60 -> N12= 11,54*cos60 = 5,77 kN

¡Vemos que el vídeo está equivocado!

Vamos al nudo 4:

∑Fy = 0 = N14*sen60 - 10kN -N42*sen60-> Del nudo 1 = N14 = 11, 55 kN, podemos despejar N42

N42 *sen60 =  11,55*sen60-10 -> N42 =-5,77kN (mal dibujado, comprime al nudo)

∑Fx = 0 = N14*cos60 -N42*cos60 +N45 -> N45 = -11,55*cos60 +5,77*cos60 = -2,89 kN

El resto de las barras son simétricas