Buenas tardes
Hoy continuamos el tema de estructuras con doble curvatura con una en especial: el paraboloide hiperbólico.
Definición:
La denominación “paraboloide” proviene del hecho de que la variable z depende de los cuadrados de las variables x e y (parábolas). Mientras que el adjetivo “hiperbólico” se debe a que a valores constantes de z se tiene la ecuación de una hipérbola. La forma de esta superficie es similar a la de una silla de montar a caballo.
Propiedades:
El Paraboloide Hiperbólico tiene las siguientes propiedades:
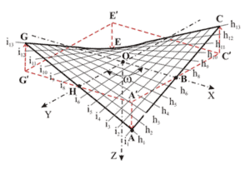
Aun siendo una superficie curvada, se puede construir con líneas rectas.
Dados cuatro puntos en el espacio que no estén en un mismo plano, hay un único paraboloide hiperbólico que pasa precisamente por estos cuatro puntos.
Aplicaciones;
El Paraboloide Hiperbólico ha sido una de las superficies que más se han aplicado en arquitectura. Gaudí fue uno de los que la emplearon, pero quien más la ha trabajado ha sido Félix Candela. Dentro de la fauna de las superficies, esta curva es un espécimen ya conocido por los griegos.
La propiedad realmente importante, que motivó el interés tanto de Gaudí como de Candela, es el hecho de que el paraboloide hiperbólico, aun siendo una superficie curvada, se puede construir con líneas rectas. Lo único que se tiene que hacer es ir variando el ángulo de inclinación de una recta que se mueve encima de otra curva. Este tipo de superficies los geómetras las denominan superficies regladas y existen ejemplos en cantidad suficiente en otro arte, en la escultura.
Es de suponer que esta propiedad es la que permitía a Gaudí dar las instrucciones precisas a sus obreros y al capataz cuando éstos tenían que construir un paraboloide hiperbólico en el techo de la Sagrada Familia (iniciada el año 1883).
Gaudí utilizó el paraboloide hiperbólico y también otras superficies doblemente regladas como el Hiperboloide de revolución. El arquitecto de origen español, exiliado a México y después nacionalizado norteamericano, Félix Candela fue quien mostró una maestría sublime en su utilización.
Restaurante Los Manantiales (1958) del parque de Choximilco en la ciudad de México. El techo está formado por ocho paraboloides hiperbólicos.
La misma estructura se puede encontrar ahora en el nuevo Oceanogràfic (2002) de la Ciudad de las Artes y de las Ciencias de Valencia.
Otro ejemplo fue El Parque_Güell diseñado por el arquitecto Gaudí con códigos del estilo modernismo catalán, con cubiertas de bóvedas catalanas en forma de paraboloide hiperbólico.
Construcción:
Dados cuatro puntos en el espacio que no estén en un mismo plano, hay un único paraboloide hiperbólico que pasa precisamente por estos cuatro puntos. Ésta es la misma propiedad que dice que dos puntos determinan una única recta.
Lo que tenían que hacer los obreros era unir con sendas barras uno de los pares de puntos de una parte, y el otro par opuesto por la otra. Después sólo se tiene que dejar resbalar otra barra sobre las dos anteriores manteniendo una velocidad constante en los extremos.
A continuación podemos ver la la construcción de una maqueta con forma de paraboloide hiperbólico:



No hay comentarios:
Publicar un comentario